Original Problem Set (Someday I’ll write them out!)
原题集 (总有一天我会写出来的!)
Q.A DanceRev
问题 A: 舞蹈革命
Problem Description
问题描述
Dance Revolution is the pioneering series of the rhythm and dance genre in video games.
The core games involve placing your feet on certain tiles according to the instruction on screen.
Here you will have four tiles: up, down, right, and left. You can move your leg one at a time. Initially, you can place your feet on any tile. Instructions will contain the list of tiles, where you must place one of your feet, one instruction after another.
Given the instruction to place your feet, find the minimum number of times you must move your legs to different tiles following the instruction. You can start with placing your legs at any position.
《Dance Revolution》(热舞革命)是电子游戏中节奏与舞蹈类游戏的开创性系列。 其核心玩法是根据屏幕上给出的指示,将脚放在特定的方块上。 在这个游戏里,设有上 下 右 左四个方块。玩家每次可以移动一条腿,一开始,脚可以放在任意一个方块上。指令会罗列出方块的相关信息,玩家需要依照顺序将脚依次放在这些方块上。 根据放置脚的相关指令,找出按照指令将脚移动到不同方块的最少次数。玩家可以从任意位置开始操作。
Given the instruction to place your feet, find the minimum number of times you must move your legs to different tiles following the instruction. You can start with placing your legs at any position.
根据放置脚的相关指令,找出按照指令将脚移动到不同方块的最少次数。玩家可以从任意位置开始操作。
Constraints
约束条件
1 <= N <= 80
Input
输入
First line consists of single integer N representing the total number of instructions.
Next N lines consist of the instructions.
第一行包含一个整数 N,代表指令的总数。 接下来的 N 行是具体的指令内容。
Output
输出
Single integer representing the minimum number of times you must move your legs.
输出一个整数,用以表示必须移动脚的最少次数。
Time Limit (secs)
时间限制(秒)
1
Examples
示例
Example 1
示例 1
Input
输入
6
down
right
down
up
right
downOutput
输出
2Explanation
解释
Assume you initially started with your legs on tiles down and right.
| Instruction | Legs position | Legs moved |
|---|---|---|
| down | down right | 0 |
| right | down right | 0 |
| down | down right | 0 |
| up | up right | 1 |
| right | up right | 1 |
| down | up down | 2 |
You must move your legs a minimum of 2 times to follow the instructions.
假设一开始你的双脚分别放在下和右这两个方块上。
| 指令 | 双脚位置 | 双脚移动次数 |
|---|---|---|
| down | down right | 0 |
| right | down right | 0 |
| down | down right | 0 |
| up | up right | 1 |
| right | up right | 1 |
| down | up down | 2 |
要按照指令进行操作,你必须移动双脚的最少次数是 2 次。
Example 2
示例 2
Input
输入
8
up
right
down
up
up
down
right
leftOutput
输出
3Explanation
解释
Assume you initially started with your legs on tiles "up" and "right".
| Instruction | Legs position | Legs moved |
|---|---|---|
| up | up right | 0 |
| right | up right | 0 |
| down | up down | 1 |
| up | up down | 1 |
| up | up down | 1 |
| down | up down | 1 |
| right | down down | 2 |
| left | right left | 3 |
You must move your legs a minimum of 3 times to follow the instructions.
假设一开始你的双脚分别放在上和右这两个方块上。
| 指令 | 双脚位置 | 双脚移动次数 |
|---|---|---|
| up | up right | 0 |
| right | up right | 0 |
| down | up down | 1 |
| up | up down | 1 |
| up | up down | 1 |
| down | up down | 1 |
| right | down down | 2 |
| left | right left | 3 |
要按照指令进行操作,你必须移动双脚的最少次数是 3 次。
Q.B JustifyWords
问题 B: 对齐单词
Problem Description
问题描述
Given a list of K words and integers N and M, you are asked to arrange the words into N lines following the below rules.
- Each line can contain no more than M letters.
- Each word should present entirely on one line.
- If multiple words are on a line, they should be separated by a single space.
Find the maximum number of words you can arrange in the given lines of length M.
给定一个包含 K 个单词的列表和两个整数 N 和 M,要求将这些单词排列到 N 行中,需遵守以下规则:
- 每行最多包含 M 个字母。
- 每个单词应完整显示在一行上。
- 如果一行上有多个单词,它们之间应该用一个空格分隔。
找出在长度为 M 的 N 行中可以安排的最多单词数量。
Constraints
约束条件
- 0 < K < 25
- 0 < N < 10
- 0 < M < 10
Words will be having only lowercase alphabets.
单词只包含小写字母。
Input
输入
First line consists of an integer K denoting the total number of words. Next K lines consist of words. Last line consists of two space separated integers denoting the values of N and M.
第一行包含一个整数 K,表示单词的总数。 接下来的 K 行是具体的单词。 最后一行包含两个用空格分隔的整数,表示 N 和 M 的值。
Output
输出
Print a single integer denoting the maximum number of words that can be arranged into the N lines.
输出一个整数,表示在 N 行中可以安排的最多单词数量。
Time Limit (secs)
时间限制(秒)
1
Examples
示例
Example 1
示例 1
Input
输入
8
i
hello
how
going
u
whatsapp
help
hmm
5 5Output
输出
7Explanation
解释
8 words need to be arranged in 5 lines each of length 5 characters. One way to arrange the words to fit maximum words is as follows.
how_i
going
u_hmm
help_
hello_where _ represents empty space. 7 words can be fitted. And that’s the maximum possible. Also there could be other combinations as [hello, help, going, i, u, hmm] etc, but what we are interested in is the maximum words that can be fitted in the given lines of length M and N rows.
8 个单词需要排列在 5 行中,每行 5 个字符。 一种可以最大化排列单词的方法如下:
how_i
going
u_hmm
help_
hello_其中 _ 表示空格。可以安排 7 个单词,这是最大可能的安排方式。也可能存在其他组合,如 [hello, help, going, i, u, hmm] 等,但我们感兴趣的是在每行长度为 M 的 N 行中容纳最多的单词数。
Example 2
示例 2
Input
输入
6
a
is
b
be
it
a
5 4Output
输出
6Explanation
解释
6 words need to be arranged in 5 lines each of length 4 characters. One way to arrange the words to fit maximum words is as follows.
a_is
b_be
it_a
____where _ represents empty space. Here the entire last line is empty. 6 words can be fitted and that’s the maximum.
6 个单词需要排列在 5 行中,每行 4 个字符。 一种可以最大化排列单词的方法如下:
a_is
b_be
it_a
____其中 _ 表示空格。这里整整一行是空的。可以排列 6 个单词,这是最大的可能安排。
Q.C FaultySegment
问题 C: 故障数码管
Problem Description
问题描述
Gagan, along with his friend, recently launched a small firm that manufactures basic calculators, which use seven-segment displays to show results.
One day, an employee brought a faulty calculator to Gagan, reporting that it was giving incorrect results due to a software glitch. After analyzing its behavior, Gagan discovered that it wasn’t a software issue but rather a flaw in the 7-segment display, where one of the LEDs was malfunctioning.
So, Gagan thought of finding the LED which is malfunctioning.
The calculator only has buttons for the digits 0-9 and the symbols +, -, *, ÷, and =. When clicked, these buttons will display their respective symbols as a seven-segment display, represented by a 3x3 matrix.
The arrangement of 7 segment display for each number from 0-9 and for the five mathematical operators is shown below.
Gagan 和他的朋友最近创办了一家小公司,生产使用七段显示器显示结果的基础计算器。
一天,一名员工向 Gagan 报告说一台计算器出现了故障,显示错误结果,怀疑是软件问题。然而,在分析后,Gagan 发现这不是软件的问题,而是七段显示器中的一个 LED 出现了故障。
于是,Gagan 想到了找出故障的 LED。
计算器只有 0-9 数字按钮和 +, -, *, ÷, = 符号按钮。点击这些按钮时,这些符号将以七段显示的形式显示,表示为 3x3 矩阵。
0-9 每个数字和五个数学运算符的七段显示安排如下:

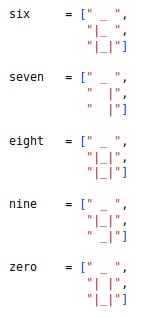

Given the equation that Gagan typed and the current display on the calculator, determine which character corresponds to the LED that should be toggled to make the equation correct.
Note: Solve the equation sequentially from left to right, without considering the precedence of operators.
根据 Gagan 输入的等式和当前计算器上的显示,确定应切换哪个字符对应的 LED 以使等式正确。
注意: 从左到右按顺序求解方程,不考虑运算符的优先级。
Constraints
约束条件
- 5 ≤ N ≤ 30
- It is guaranteed that RHS or the equal to symbol will not be faulty.
- RHS will not have any operators.
- It is guaranteed that all the test cases will have only one solution.
- 5 ≤ N ≤ 30
- 保证右侧结果或等号符号不会出错。
- 右侧结果不会有任何运算符。
- 保证所有测试用例只有一个解决方案。
Input
输入
- First line consists of N denoting the number of characters in the given equation.
- Next 3 lines will have the 7-segment display of the equation which Gagan typed.
- 第一行包含一个整数 N,表示给定方程中的字符数。
- 接下来的 3 行将显示 Gagan 输入的方程的七段显示。
Output
输出
- Print the position corresponding to the faulty character displayed. Count starts from one.
- 输出表示错误字符位置的整数。计数从一开始。
Time Limit (secs)
时间限制(秒)
1
Examples
示例
Example 1
示例 1
Input
输入
5
_ _
||_ _| _ |_|
|| |_ _ _|Output
输出
1Explanation
解释
After processing each character (represented as a 3x3 matrix), we get the equation 1+2=9, which is incorrect. To correct it, we need to toggle one LED in the first character (1) to make it 7, resulting in the correct equation 7+2=9. Since the error is in the first character, print 1.
在处理每个字符(表示为 3x3 矩阵)后,我们得到等式 1+2=9,这是不正确的。要纠正它,我们需要切换第一个字符(1)中的一个 LED 使其变为 7,从而得到正确的等式 7+2=9。由于错误在第一个字符,所以输出 1。
Example 2
示例 2
Input
输入
6
_ _
_||_ _| _ | |
|_ | _| _ | |Output
输出
3Explanation
解释
After processing each character (represented as a 3x3 matrix), we get the equation 2+3=11, which is incorrect. To correct it, we need to toggle one LED in the third character (3) to make it 9, resulting in the correct equation 2+9=11. Since the error is in the third character, print 3.
在处理每个字符(表示为 3x3 矩阵)后,我们得到等式 2+3=11,这是不正确的。要纠正它,我们需要切换第三个字符(3)中的一个 LED 使其变为 9,从而得到正确的等式 2+9=11。由于错误在第三个字符,所以输出 3。
Q.D Bands
问题 D: 手环
Problem Description
问题描述
Two friends went to the mall for shopping. While there, they decided to buy friendship bands.
The shop sells bands in pairs in a case, which is exactly what they wanted. These bands could be of different shapes and sizes. These band pairs were displayed in a transparent box inside the shop. While most of them were fine i.e., two distinct and separate bands, in some cases the pairs of bands encased in the transparent box were not separate but were interlocked instead. Now, the bands should not be interlocked because that would mean cutting one of them to separate the two. However, there were complaints regarding the same.
They did not want to miss out on celebrating Friendship Day and desperately wanted the bands. Since the bands were packed in transparent cases, they could see the bands. They decided to select a good pair of bands from the cases.
They took photos of the cases and fed it to an AI program that could mathematically detect if there was interlocking between bands or not. The band case is represented in a square matrix format of size S. The bands are depicted by the characters 1 and 2 where they represent the first and second band, respectively. The period . indicates an empty space.
The bands will only bend at right angles. One band will intersect the other exactly at a right angle, but they will never overlap at the corners. The character at the point of overlap indicates which band is on top, while the other character’s band is underneath. To avoid confusion for them, the bands will not be kept adjacent and there will be some space between them i.e., if a thread is running horizontal, then another thread will not run horizontal on the adjacent cells. Vice versa for vertical also. The below images represent how the bands would not be interlocked.
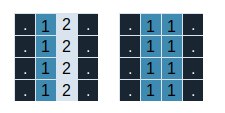
Now, instead, it would look like below…
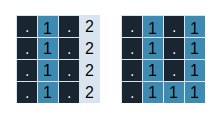
The image below is an example of the case and the bands inside it.
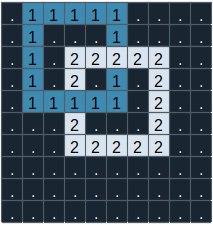
Help the friends choose a case with non - interlocked bands i.e., check whether the given case with bands can be separated without cutting one of the bands.
两位朋友去商场购物。在那里,他们决定购买友谊手环。
商店将手环成对装在盒子里出售,这正是他们想要的。这些手环可能有不同的形状和大小。这些手环对在商店内的透明盒子里展示。虽然大多数手环对都是正常的,即两条不同且分开的手环,但在某些情况下,装在透明盒子里的手环对不是分开的,而是相互缠绕的。现在,手环不应该相互缠绕,因为那样就意味着要剪断其中一个才能将它们分开。然而,关于这个问题存在一些投诉。
他们不想错过庆祝友谊日的机会,非常想要买到手环。由于手环装在透明盒子里,他们可以看到手环。他们决定从这些手环对中挑选出一对好的。
他们拍下了这些手环对的照片,并将其输入到一个人工智能程序中,该程序可以通过数学方法检测手环之间是否相互缠绕。手环对以大小为S的方阵形式表示。手环用字符1和2表示,分别代表第一只和第二只手环,.表示空白空间。
手环只会在直角处弯折。一只手环会与另一只手环正好在直角处相交,但它们在拐角处不会重叠。在交叉点处的字符表示哪只手环在上面,另一只手环在下面。为了避免混淆,手环不会相邻放置,它们之间会有一些空隙,即如果一根线是水平走向的,那么相邻的线在相邻的单元格不会是水平走向的,垂直方向也是如此。下面的图片展示了手环不相互缠绕的情况。

相反,它看起来会像下面这样……

下面的图片是这种情况和里面手环的一个示例。

帮助朋友们选择没有相互缠绕的手环对,即检查给定的手环对是否可以在不剪断其中一个手环的情况下分开。
Constraints
约束条件
5 ≤ S ≤ 25
5 ≤ S ≤ 25
Input
输入
- First line consists of an integer S representing the side of the square matrix.
- Next S lines will consist of S characters either '.', '1' or '2' representing the case with bands.
- 第一行包含一个整数S,表示方阵的边长。
- 接下来的S行每行包含S个字符,字符为"."、"1"或"2",表示带有手环的情况。
Output
输出
Single integer denoting the number of overlaps if bands can be separated without cutting, else print 'Impossible'
单个整数,表示如果手环可以不剪断分开的重叠数量,否则打印"Impossible"
Time Limit (secs)
时间限制(秒)
1
Examples
示例
Example 1
示例 1
Input
输入
10
.111111...
.1..1.....
.1.22122..
.1.2.1.2..
.11211.2..
..2..2....
...22222..
...........
...........Output
输出
ImpossibleExplanation
解释
The image below depicts the input described above.
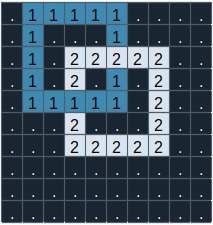
From the image it is easy to see that the two bands cannot be separated without cutting any one of it. Hence print Impossible.
下图描述了上述输入。

从图像中可以很容易地看出,这两只手环不剪断其中任何一个就无法分开。因此打印Impossible。
Example 2
示例 2
Input
输入
10
.111111...
.1..1.....
.1.22122..
.1.2.1.2..
.11211.2..
..2..2....
...22222..
...........
...........Output
输出
2Explanation
解释
The image below depicts the input described above.
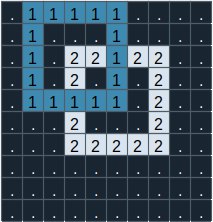
The band 1 is just placed above the band 2. They are not interlocked and can be separated without cutting. Since they are overlapping at two positions, the output is 2.
下图描述了上述输入。

手环1正好在手环2的上方。它们没有相互缠绕,可以不剪断就分开。由于它们在两个位置重叠,所以输出是2。
Example 3
示例 3
Input
输入
12
.............
.11111111...
.1......1...
.1.111111...
.1.221222...
.1.2.1.222.
.1.221.2...
.1.1......1
.11111111..
.............
.............Output
输出
2Explanation
解释
The image below depicts the input described above.

The band 1 is just placed above the band 2. They are not interlocked and can be separated without cutting. Since they are overlapping at two positions, the output is 2.
下图描述了上述输入。

手环1正好在手环2的上方。它们没有相互缠绕,可以不剪断就分开。由于它们在两个位置重叠,所以输出是2。
Q.E Magic Stars Intensity
问题 E: 魔法星星强度
Problem Description
问题描述
In the 1930s, Krishnamurthy, who had a great love for magic, kept a personal magician in his palace. Whenever he desired to witness a magical performance, he would command the magician to entertain him with his craft.
The magician always aimed to impress the king with new magical tricks. One day, he cast magical lines across the vast expanse of the palace floor, which was covered in tiles. Each tile is a square with sides of 1 unit length; thus, you can say the palace floor resembles a 2D plane.
Since these are magical lines, when they are drawn, they only align with the edges of the tiles or pass through their corners.
When these magical lines intersect, they create points of light called "stars", where n ranges from 2 to 8. Each star’s brightness is determined by the number of lines that intersect at that point, and all these stars generate light.
For calculating the intensity of the stars, there exist two cases which are explained below.
Consider the following cases carefully:
Case 1 - The line is only one side to the star i.e., the star lies out the line in one part.
Consider the lines (4, 4, 2, 4), (4, 4, 7, 7) and (4, 4, 3, 5). These lines are intersecting at the point (4, 4). Since three lines intersect at a point, they form a star known as a 3 - star.
Now, the intensity of the star = minimum (the number of cells these 3 lines are touching from the point of star formation to the last) = minimum(2, 3, 1) = 1.
So, the intensity of this star will be 1.
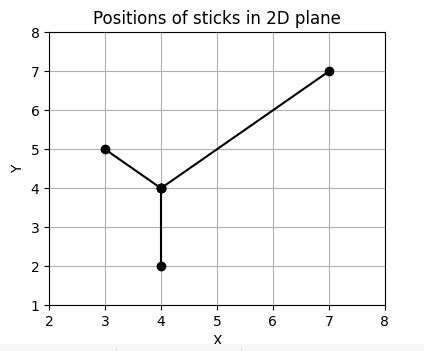 杆在2D平面中的位置
杆在2D平面中的位置
Case 2 - The line is two sides to the star i.e., the star cuts the line into two parts.
Consider the lines (3, 3, 7, 7), (3, 3, 5, 6) and (4, 4, 4, 6). These lines are intersecting at the point (4, 4). Since three lines intersect at a point, they form a star known as a 3 - star.
In this case, the intensity of the star = minimum (the number of cells these 3 lines are touching from the point of star formation to the last on both sides) = minimum(1, 1, 2, 2, 3, 2) = 1.
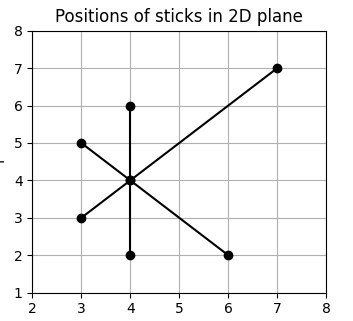 杆在2D平面中的位置
杆在2D平面中的位置
Given N lines and the type of star for which you need to calculate the intensity, calculate the intensity for all such stars according to the cases described and print their total sum. If no stars of the specified type are present, print 0.
在20世纪30年代,克里希那穆提(Krishnamurthy)非常热爱魔术,他在自己的宫殿里养了一名私人魔术师。每当他想看魔术表演时,他就会让魔术师表演魔术来娱乐他。
魔术师总是想用新的魔术技巧给国王留下深刻印象。有一天,他在铺满瓷砖的宫殿大厅的广阔地面上画了魔法线。每块瓷砖是边长为1单位长度的正方形,所以可以说宫殿的地面就像一个二维平面。
由于这些是魔法线,当它们被画出来时,它们只会沿着瓷砖的边缘或者穿过瓷砖的角。
当这些魔法线相交时,它们会产生被称为"星星"的光点,n的范围从2到8。每颗星星的亮度由在该点相交的线条数量决定,并且所有这些星星都会发光。
为了计算星星的强度,有以下两种情况需要解释。
仔细考虑以下情况:
情况1 - 这条线只在星星的一侧,即星星在线的一侧。
考虑这些线(4, 4, 2, 4)、(4, 4, 7, 7)和(4, 4, 3, 5)。这些线在点(4, 4)相交。由于三条线在一个点相交,它们形成了一颗被称为3星的星星。
现在,星星的强度 = 最小值(这三条线从星星形成点到最后接触的方格数)= 最小值(2, 3, 1) = 1。
所以,这颗星星的强度将是1。
 杆在2D平面中的位置
杆在2D平面中的位置
情况2 - 这条线在星星的两侧,即星星把线分成两部分。
考虑这些线(3, 3, 7, 7)、(3, 3, 5, 6)和(4, 4, 4, 6)。这些线在点(4, 4)相交。由于三条线在一个点相交,它们形成了一颗被称为3星的星星。
在这种情况下,星星的强度 = 最小值(这三条线从星星形成点到最后在两侧接触的方格数)= 最小值(1, 1, 2, 2, 3, 2) = 1。
 杆在2D平面中的位置
杆在2D平面中的位置
给定N条线和你需要计算强度的星星类型,根据所描述的情况计算所有这种星星的强度并打印出它们的总和。如果没有指定类型的星星存在,打印0。
Constraints
约束条件
1 ≤ N ≤ 50 2 ≤ k ≤ 8 0 ≤ x, y ≤ 100 Lines will not overlap either partially or completely.
1 ≤ N ≤ 50 2 ≤ k ≤ 8 0 ≤ x, y ≤ 100 线条不会部分或完全重叠。
Input
输入
First line consists of an integer N denoting the number of magical lines the magician cast.
The next N lines contain four space - separated integers each, representing the x and y coordinates of the starting and ending points of the magical lines.
The last line consists of an integer k denoting the type of star for which you need to calculate the intensity.
第一行包含一个整数N,表示魔术师画出的魔法线条数。
接下来的N行每行包含四个用空格分隔的整数,分别表示魔法线起点和终点的x和y坐标。
最后一行包含一个整数k,表示你需要计算强度的星星类型。
Output
输出
Print a single integer representing the total intensity of all stars of the specified type given in the input. If no such stars are present, print 0.
打印一个整数,表示输入中给定类型的所有星星的总强度。如果没有这种星星存在,打印0。
Time Limit (secs)
时间限制(秒)
1
Examples
示例
Example 1
示例 1
Input
输入
7
4 2 4 6
5 1 1 8
8 3 1 3
4 5 1 5
8 1 3 3
7 2 2 9
2Output
输出
4Explanation
解释
The lines given in the above input are represented in the below figure.
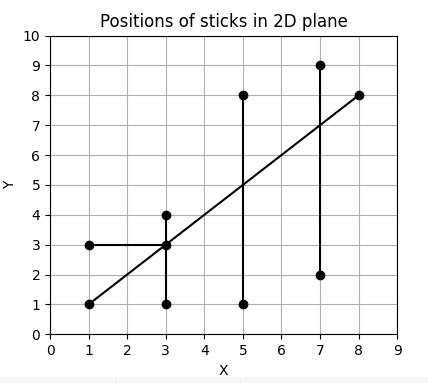 杆在2D平面中的位置
杆在2D平面中的位置
There are two 2 - stars formed at the positions (5, 5) and (7, 7). The intensity of the star at (5, 5) is minimum(4, 3, 3, 4) which is 3 and the intensity of the star at (7, 7) is minimum(1, 1, 2, 6) which is 1. So, the total intensity of all 2 - stars will be 3 + 1 = 4.
上述输入中的线条在下图中表示。
 杆在2D平面中的位置
杆在2D平面中的位置
在位置(5, 5)和(7, 7)形成了两个2 -星。在(5, 5)处星星的强度是最小值(4, 3, 3, 4)即3,在(7, 7)处星星的强度是最小值(1, 1, 2, 6)即1。所以,所有2 -星的总强度是3 + 1 = 4。
Q.F CardBox
问题 F: 卡片盒
Problem Description
问题描述
Chintu is planning to build a closed box. The raw material he chose is a square - shaped card. He will glue the edges to build a box out of it.
The square - shaped card will have an area of 1 square unit. He will only place the cards parallel to any one of the planes - xy, yz or zx.
Assuming Chintu placed the cards in a 3D coordinate system, the position of each card is given in the format
x y z axis where x, y, and z are integers representing the coordinates of the bottom - left corner of the card, and the axis indicates the plane to which the card is parallel to.
For example, consider "0 0 xy"
The above input means that card’s bottom - left corner is positioned at (0, 0) in the xy - plane. This square can be represented by the coordinates (0, 0), (0, 1), (1, 0), and (1, 1).
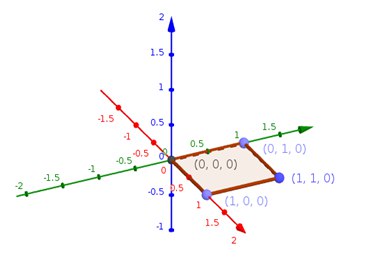
The X - axis is shown in red, the Y - axis in green, and the Z - axis in blue.
For the coordinates "0 0 yz", it can be interpreted as (0, 0), (0, 1), (1, 0), and (1, 1). The representation of the same is shown below.
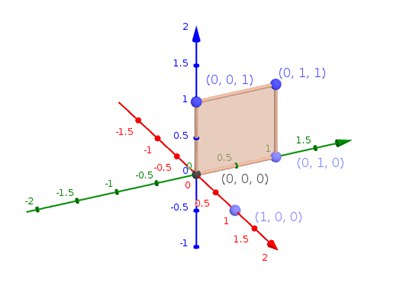
Likewise, for the coordinates "0 0 zx", it can be interpreted as (0, 0), (1, 0), (0, 1), and (1, 1), which is shown in the below.
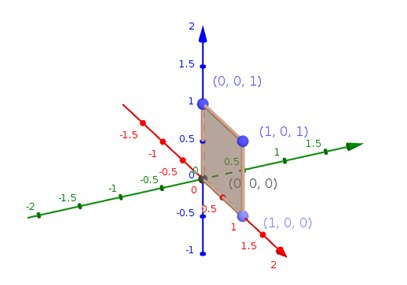
Assume Chintu either built a closed box or is at most one card short to make it a closed one. In either case, it will be a single - compartment i.e., he will not place cards such that it will dissect the space inside the boxed compartment. Given how Chintu placed the cards find and print output as mentioned below.
If the box is closed one, i.e., there is no opening present. In this case, print the volume of the box in terms of unit cubes.
Else if it has an opening, print the coordinates of the missing card in the same format mentioned in the input, which is required to make the box a closed one.
Chintu打算制作一个封闭的盒子。他选用的原材料是方形卡片,他将通过粘贴卡片的边缘来构建一个盒子。
这种方形卡片的面积为1平方单位。他只会将卡片平行于xy、yz或zx平面放置。
假设Chintu将卡片放置在一个3D坐标系中,每张卡片的位置以如下格式给出:
x y z axis 其中x、y和z是表示卡片左下角坐标的整数,轴表示卡片所平行的平面。
例如,考虑"0 0 xy"
上述输入意味着卡片的左下角在xy平面中的位置是(0, 0)。这个正方形可以由坐标(0, 0)、(0, 1)、(1, 0)和(1, 1)表示。

X轴用红色表示,Y轴用绿色表示,Z轴用蓝色表示。
对于坐标"0 0 yz",可以解释为(0, 0)、(0, 1)、(1, 0)和(1, 1),其表示如下所示。

同样,对于坐标"0 0 zx",可以解释为(0, 0)、(1, 0)、(0, 1)和(1, 1),如下所示。

假设Chintu要么构建了一个封闭的盒子,要么最多差一张卡片就能使其封闭。在任何一种情况下,它都将是一个单室结构,即他不会放置会分割盒内空间的卡片。根据Chintu放置卡片的方式,找到并按如下所述打印输出。
如果盒子是封闭的,即没有开口。在这种情况下,以单位立方体的形式打印盒子的体积。
否则,如果有开口,以输入中提到的相同格式打印缺失卡片的坐标,这是使盒子封闭所需要的。
Constraints
约束条件
5 ≤ N ≤ 30
5 ≤ N ≤ 30
Input
输入
First line consists of an integer N representing the total number of square - shaped cards placed.
The next N lines each consist of three integers representing coordinates separated by spaces, along with the plane (xy, yz, zx in lowercase) to which they are parallel.
第一行包含一个整数N,表示放置的方形卡片总数。
接下来的N行每行包含三个由空格分隔的整数,表示坐标,以及它们所平行的平面(xy、yz、zx用小写字母表示)。
Output
输出
Single integer represents the volume if it is a closed box.
Else print the coordinates of the missing card in the format "x y z plane" which if placed would make it a closed box.
如果是封闭的盒子,输出单个整数表示体积。
否则,以"x y z平面"的格式打印缺失卡片的坐标,放置该卡片可使盒子封闭。
Time Limit (secs)
时间限制(秒)
1
Examples
示例
Example 1
示例 1
Input
输入
10
0 0 xy
0 0 yz
0 0 zx
0 1 xy
0 1 zx
1 0 xy
1 0 zx
1 0 1 xy
2 0 0 yz
1 1 0 zxOutput
输出
2Explanation
解释
Placing cards as given input will look like below.
Placing cards as given input will looks like below. 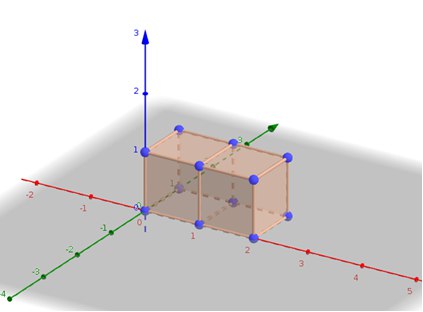
As we can see, the box is closed, and its capacity is 2 unit cubes, hence print 2.
按照输入放置卡片如下所示。
将卡片作为给定的输入放置如下所示 
如我们所见,盒子是封闭的,其体积为2单位立方体,因此打印2。
Example 2
示例 2
Input
输入
9
0 0 xy
0 0 yz
0 0 zx
0 1 xy
0 1 zx
1 0 xy
1 0 zx
2 0 0 yz
1 1 0 zxOutput
输出
1 0 1 xyExplanation
解释
Placing cards as given input will looks like below.
将卡片作为给定的输入放置如下所示 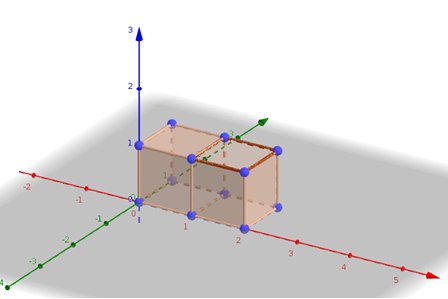
As you can see that one card is missing at the top. A card needs to be placed which should cover (1, 0, 1), (2, 0, 1), (1, 1, 0) and (2, 1, 0) and it should be parallel to xy - plane. Hence that card needs to be placed on 1 0 1 xy.
将卡片作为给定的输入放置如下所示 
如你所见,顶部缺少一张卡片。需要放置一张应覆盖(1, 0, 1)、(2, 0, 1)、(1, 1, 0)和(2, 1, 0)且平行于xy平面的卡片。因此,需要放置的卡片坐标是1 0 1 xy。
友情提示:
中文与英文版存在的差异,请以英文原文为标准。


